This initial blog post written in collaboration with my B.Sc. students Jonas Bode, Tobias Hürten, Luca Liberto , and Florian Spelter intends to give a rough outline of the key concepts of building Reinforcement Learning (RL) without using any formulas. As a result, no mathematical background is needed and even more, the key concepts are introduced naturally by addressing your intuition. While this post attempts to be fully understood without any prior mathematical knowledge, it should be noted that basic skills in calculus, probability theory, and algebra is fundamental for gaining a deep understanding of RL. But, to get you started quickly, we decided to introduce the math and equations behind RL in the second post of the series.

Motivation: Why bother with Reinforcement Learning?

Looking back to present breakthroughs in Artificial Intelligence (AI) and especially in RL, we observe rapid progress in Machine Learning (ML) without human supervision in a wide variety of domains such as speech recognition, image classification, genomics, and drug discovery. These unsupervised learning models are mainly motivated by the fact that for some problems human knowledge is too expensive, too unreliable, or unavailable. Moreover, the ambition of AI research is to bypass the need for human supervision by creating models that achieve superhuman performance without human input.

One popular example is AlphaGo, a computer program developed by researchers at Google DeepMind, which has been shown to surpass the abilities of the best professional human Go player in 2017. Very soon the model was beaten by a newer evolution of itself 100-0 without human supervision. Similar breakthroughs are to be found in the realm of E-Sports: For example, a team at OpenAI developed bots being able to beat human professionals in the highly competitive video game Dota 2 in a 5v5 game in 2019. So how not be curious about the magic behind RL? In the following, we will take you with us on a journey diving deep into the field of RL.

What is Reinforcement Learning?

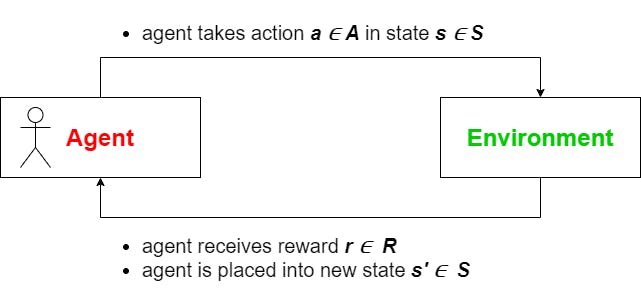
To understand the fundamentals of Reinforcement Learning it is important to understand one simple key concept: The relationship between an agent and its environment. To grasp the idea of an agent, it seems pretty natural to replace it with oneself

• a human being interacting with its surroundings, retrieving information about itself and those surroundings, and changing its state through actions over a finite time horizon. Now the human being - representing the agent - usually has quite a wide variety of different actions we could take. For example, imagine you have a walk with the dog: There are two options regarding clothing. We could either take a jacket or pass on doing so. To decide which of both options to choose, it is pretty intuitive to observe the temperature outside - the environment so to speak. But how do we know if our decision was optimal? We will receive feedback - a reward - from the environment. In our example, we might be freezing if we decided not to take the jacket and whether is quite cold or sweaty if it is too hot. And that example - at its core - represents what the relationship between agent and environment is about. More formally, the agent takes an action a in state s and collects a reward r in return to evaluate choice a, given the current state s. Finally, the system transitions into the next state s', which is determined by a transition function P.

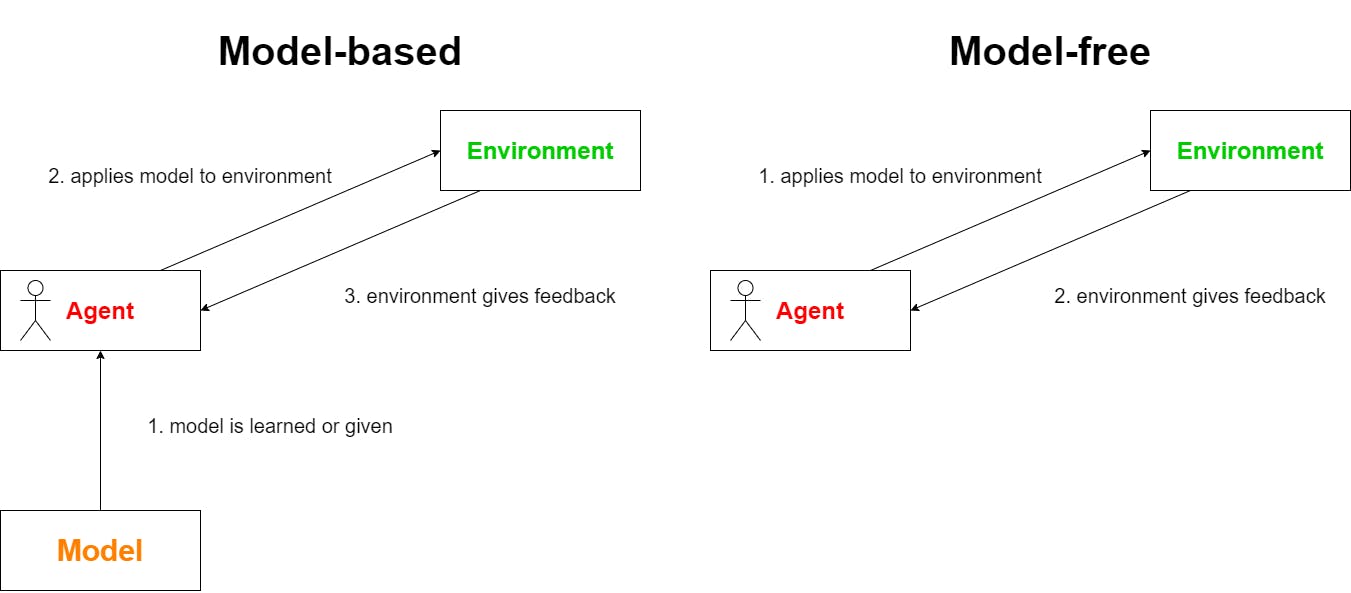
Model-based vs model-free

After introducing the key concept of the "agent - environment" relationship, we can introduce the two most basic cases regarding the agent's knowledge about the model describing its environment: Simply, knowing the model and not knowing the model.

Imagine a world, in which the weather is sunny exactly every other day and rainy on every remaining day. If our agent has to do some work outside, but can freely decide on which day he works on the respective tasks, knowing the world's model will probably cause the agent to work outside mostly on sunny days for a better outcome. On the other hand, if the model is not known to the agent he will probably finish his work on the first day to collect the reward, thus completing the task as soon as possible and learning the environment model as part of the learning experience itself.

In formal terms, we distinguish between model-free and model-based RL, meaning that in model-based RL, the model is known to the agent. This is why model-based problems can be solved using "simpler" algorithms and by Dynamic Programming (DP). In comparison, model-free RL enforces the agent to learn the environment model as part of solving the learning problem.

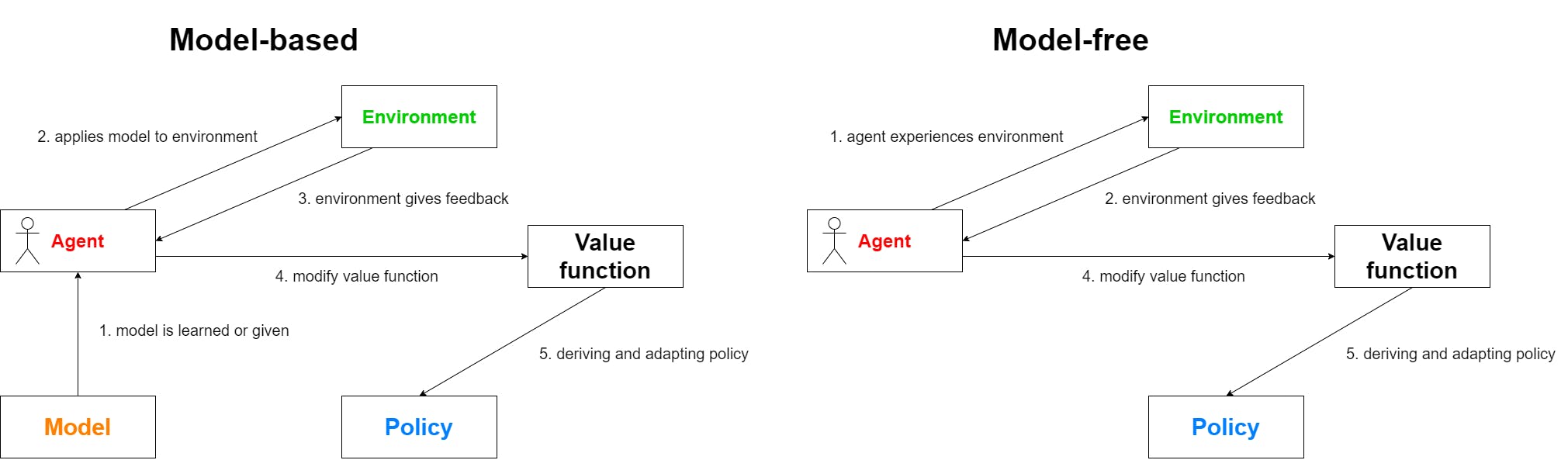
Policies

A policy \(\pi\) describes the strategy by which the agent chooses which actions to take in which state. The optimal policy returns the best possible action for each state to receive the biggest possible reward. Furthermore we differentiate a deterministic policy \(\pi\)(s) and a stochastic policy \(\pi\)(a|s) which returns the action based on a probability given that the agent is in state s.

Value functions

Given state s it doesn't seem too practicable to brute force action a and see what the reward will be. Instead, we should try to predict the future rewards for each possible state-action pair (s,a). To get a better understanding of this approach let us take a look at another example from everyday life.

State: Having an amount of money in your bank account.

Action 1: Withdraw the money now to buy yourself something.

Action 2: Leave the money in your bank account to earn more money through interest and buy yourself something more expensive in the future.

Both of these actions result in a certain reward. The key difference is that if you only consider the rewards up to the current time, action 1 has a much higher reward because you would buy yourself something right away while action 2 would reward you with nothing. But, action 2 will grant you a much higher reward in the future and this reward may outweigh the reward of action 1. The main point to look at when deciding between actions 1 and 2 is, whether waiting the additional time is worth the higher reward or not. And this is the major idea behind value functions.

Value functions are mostly referred to as V(s(t)) with s(t) being the current state. The idea behind this function is to observe future states s(t+1), s(t+2)... and predict their corresponding rewards. In other words, the value function quantifies how good a state is. Both policy and value functions are what we try to learn in reinforcement learning.

As a result, the value function is computed by the future reward, also known as return, which is a total sum of discounted rewards going forward. The discount factor, also denoted by \(\gamma\), is used to discount future rewards to not wait indefinitely or prefer rewards we receive in the near future. Back to our example, in case we wouldn´t have such a discount factor, we might wait endlessly to buy a house because its reward would outweigh the rewards of all daily expenses like buying food for example.

Now we can use these value functions to update our policies converging to the optimal policy. We will encounter this principle as value iteration in a later post.

References 📚

• Cover Image: Cover Image
• Blog by Lilian Weng: Lil'Log