
Photo by Elena Popova on Unsplash
AlphaGo Zero Explained
Mastering the Game of Go without Human Knowledge
In October 2015 DeepMind's AlphaGo Fan beat the European Go champion Fan Hui in the game of Go decisively and just one year later AlphaGo Lee defeated Lee Sedol who is considered to be one of the greatest Go players of the past decade. This demonstrates the potential of RL algorithms to outperform humans in a complex game that requires strategy and forethought. Since then, DeepMind has continued to improve the architecture behind AlphaGo, developing new versions with dramatically greater performance. One such recent variation, dubbed AlphaGo Zero, has surpassed all previous versions of AlphaGo in a relatively short time.
This blog post aims to provide a fundamental knowledge of the AlphaGo Zero architecture and the elegance of its interactions between used algorithms.
The game of Go
The game of Go (围棋) is an ancient game originating in China more than 3000 years ago. Like chess, Go has very simple rules but requires dramatically different thinking to master. The objective of the game is to surround as much territory on the board as possible by placing white and black stones (one player uses black, the other white) sequentially on intersections (called "points") of a 19x19 grid. Unlike chess, however, there are no restrictions on where to place the first stone.
Additionally, points surrounded wholly by one color are called "territories" and associated with that color's player.
As you can see below only the dark areas are controlled by Black while White controls all bright areas:

Go differs from chess in that the number of moves possible is greater, but the minimum number of moves it takes to capture enemy pieces (a "group") is fewer than in chess.
The game starts with an empty board and both players alternately place stones on unoccupied intersections until they pass their turn. The game ends when both players pass without any territory being captured or one player concedes defeat.
Go is a perfect example for applying RL algorithms since there are no restrictions on where you can place your stone next. Additionally, Go has deep complexity meaning that if you want to beat the best human players you need to think even further ahead than they do! For more details on how AlphaGo Fan achieved this check out their original paper.
The outstanding idea behind AlphaGo Zero
The main distinction between AlphaGo Zero and its predecessors AlphaGo is that it has no prior human knowledge or supervision, therefore it is essentially starting from the ground up (or as some would say "tabula rasa"), which roughly translates to a blank or clean slate.
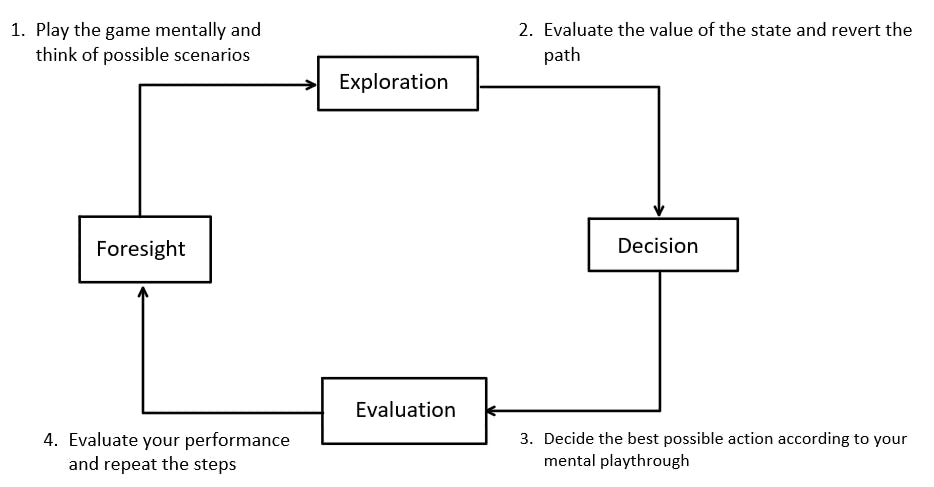
To better understand AlphaGo Zero's concept, let's break it down into simple steps. The appeal of AlphaGo Zero is that the fundamental concept is precisely how we would attempt to play a game without any prior knowledge by just knowing the rules.
Foresight
Consider a game board in front of you. The first thing we'd do is look at potential scenarios that might affect the game's outcome. Naturally, the most important consideration is which route or state would provide us the greatest advantage and our opponent's reaction to our own actions. We obviously can't always anticipate every move our opponent will make or how the game will develop as a result of taking an action correctly, but it does give us a good sense of what may happen.
Exploration
We record the results of our operations and compare them to previous actions in order to verify their efficacy. Every time we reach a new state, we want to know how important it is and whether there are any patterns in our path that might be used in later matches or even years down the road. The value of a state can vary during your journey and over time as you play and re-assess.
Decision
When we've finished analyzing and playing through all of the potential states and paths, we take an action based on our knowledge of the game, which means we'll choose the course of action that we've explored the most since this would be the route with which we have acquired the most information. Our decisions in a given state might differ and alter as a result of learning and increasing expertise.
Evaluation
In the final analysis, which takes place at the end of the game, we must evaluate our performance in the game by assessing our blunders and misjudgments on a state-by-state basis for the goals of those states. We should also look at where we got it right so that we may repeat this successful step again. After that, we have a greater knowledge of the game and can get ready for the next match with our new awareness.
Reinforcement Learning in AlphaGo Zero
AlphaGo Zero utilizes two main components, a deep neural network \(f_\theta\) with parameters \(\theta\) and a Monte Carlo tree search algorithm (MCTS). The deep neural network takes the raw board representation of the current board combined with previous board states into one state \(s\) as input to predict a probability for each move of the given board state, encoded as a vector \(p\), and to predict the chance of victory \(v\) for the current player, \((p, v) = f_\theta(s)\). The resulting combination of move (action) \(a\) given inboard state \(s\) is called state-action pair and can be defined by the tuple \((s, a)\).
When asked to choose its next move \(a\) inboard state \(s\), the algorithm will conduct an MCTS using the deep neural network. This utilizes a tree in such that the nodes of the tree are defined by the board states \(s\) and the edges represent the state-action pairs \((s, a)\).
Moreover, each edge contains a counter \(N(s, a)\) that counts how frequently the edge was chosen during the search. The edge also contains a value \(P(s, a)\), calculated from the neural network probability \((P(s, \cdot), V(s)) = f_\theta(s)\) . Note that the neural network also provides us with a current board state value function \(V(s)\). Finally, each edge includes the action value \(Q(s, a)\) derived from the resulting board state value function \(V(s')\) after executing action \(a\).
To summarize, each edge \((s, a)\) currently has three values \(N(s, a), P(s, a), Q(s, a)\) and we can calculate the state-action pair's promise as \(Q(s, a) + U(s, a)\), in which \(U(s, a) \propto \frac{P(s, a)}{N(s, a) + 1}\) is the balance between exploration and exploitation.
Assuming that \(s_0\) is the board state when we start the MCTS, the tree search is composed of the following steps:
Initialize the tree with a single node: The current board state \(s_0\) and its edges are defined by \((s_0, a)\).
Follow the most promising route, which is to say, always choose to follow the edge with the greatest value of \(Q(s, a) + U(s, a))\), until an edge \((s, a)\) is selected that leads to a board state \(s'\) that has not yet been recorded in the tree. (Step 1 in the idea diagram)
Expand the tree by creating a separate node for the new board state \(s'\), and increase the counter \(N(s, a)\) as well as update \(Q(s, a)\) for each edge leading to this new board position. (Step 2 in the idea diagram)
If it is anticipated that the movement will be selected within a limited amount of time, advance to step 2. Else return a stochastic policy \(\pi(a | s_0) \propto N(s_0, a)^{\frac{1}{\tau}}\) using the hyperparameter \(\tau\), meaning that the resulting policy \(\pi(a | s_0)\) recommends moves by assigning probabilities to actions.
Derive the next move from policy \(\pi(a | s_0)\). (Step 3. in the idea diagram)
The resulting policy \(\pi(a | s_0)\) can be viewed as a refinement of the raw network output probatilites \(p\) with \((p, v) = f_\theta\).
This technique allows the algorithm to play against itself multiple times. After each self-play match has concluded, the match history may be used to construct multiple triples: \((s, \pi(\cdot| s), z)\) where \(s\) is a board state, \(\pi(\cdot| s)\) is the MCTS move probabilities for this board state, and z is an encoding of the ultimate winner of the match \(z\) (i.e., did the player whose turn it was in the board state \(s\) win?).
After multiple of these self-plays have concluded, a batch from the available triples is chosen to be used in training the deep neural network. The network is trained for each triple \((s, \pi(\cdot| s), z)\) in the batch. The training minimizes the error between the network output, the MCTS policy and the eventual winner so that \(f_\theta(s) = (p, v) \sim (\pi(\cdot| s), z)\). (Step 4. in the idea diagram)
The whole process can be visualized as follows:
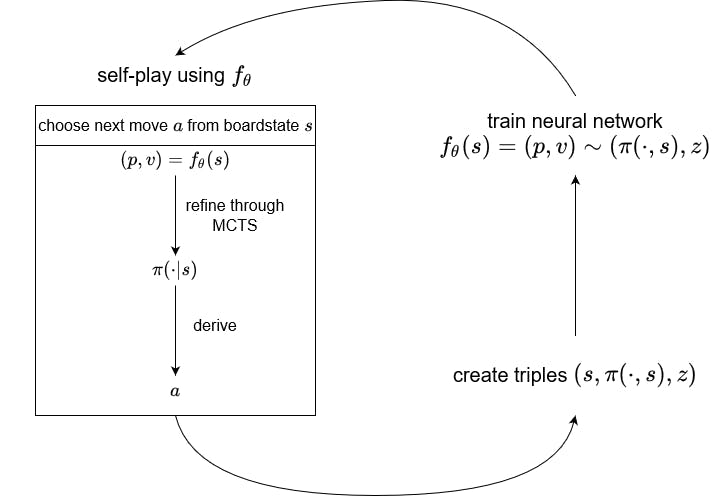
The deep neural network deployed in AlphaGo Zero is a residual neural network (ResNet). In particular, the neural network in the original paper consisted of 40 residual blocks. These blocks were all initialized randomly, meaning AlphaGo started learning without any prior knowledge and thus learned only by using the self-play mechanism, requiring no human supervision.
Results achieved by AlphaGo Zero
AlphaGo Zero quickly outperformed previous iterations of AlphaGo, even while beginning with significantly lower performance than a supervised RL approach. This is demonstrated in the graph from the original paper linked below, which compares the training performance to supervised learning and Alpha Go Lee, the version that defeated Sedol, a grandmaster player.
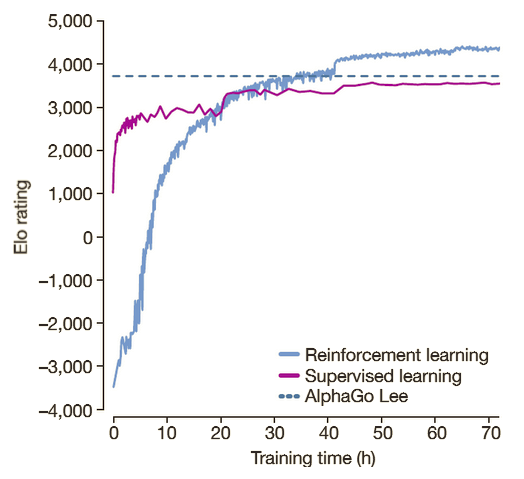
An Elo rating is used to compare the various methods. The new RL approach surpasses the original supervised learning technique after around 20 hours, according to the graph. It surpassed AlphaGo Lee's Elo rating 16 hours later as well. After a total of 72 hours, the learning phase was completed, and AlphaGo Zero beat AlphaGo Lee in a final clash of 100 matches without losing once.
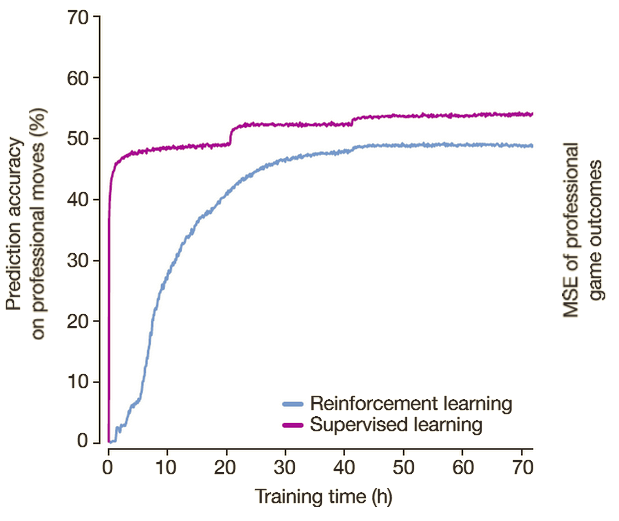
Another interesting side note about the accuracy of professional human players' moves is that AlphaGo Zero learns different gaming strategies and methods, predicting human actions with less accuracy than supervised learning. The graph below demonstrates this fact: While never reaching supervised learning's accuracy of approximately 50%, AlphaGo Zero improves on this aspect. Researchers were also able to discover new enhanced versions of previous methods.
All of this indicates that RL algorithms could be used in a wide range of fields and that RL solutions might compete and even outperform human knowledge acquired over hundreds of years. The research team's efforts, however, are not yet complete. In this instance, the learning technique was utilized to play the popular game Go, but it may also be applied to a variety of games and problems. As a result, the following section will borrow AlphaGo's approach for another type of model: Connect Four - demonstrating the method's flexibility.
Exemplary results
By exchanging the model - in this case, the rules of Go to Connect Four - and applying the discussed AlphaGo Zero learning approach the following results were observed over 78 iterations with 30 episodes each:
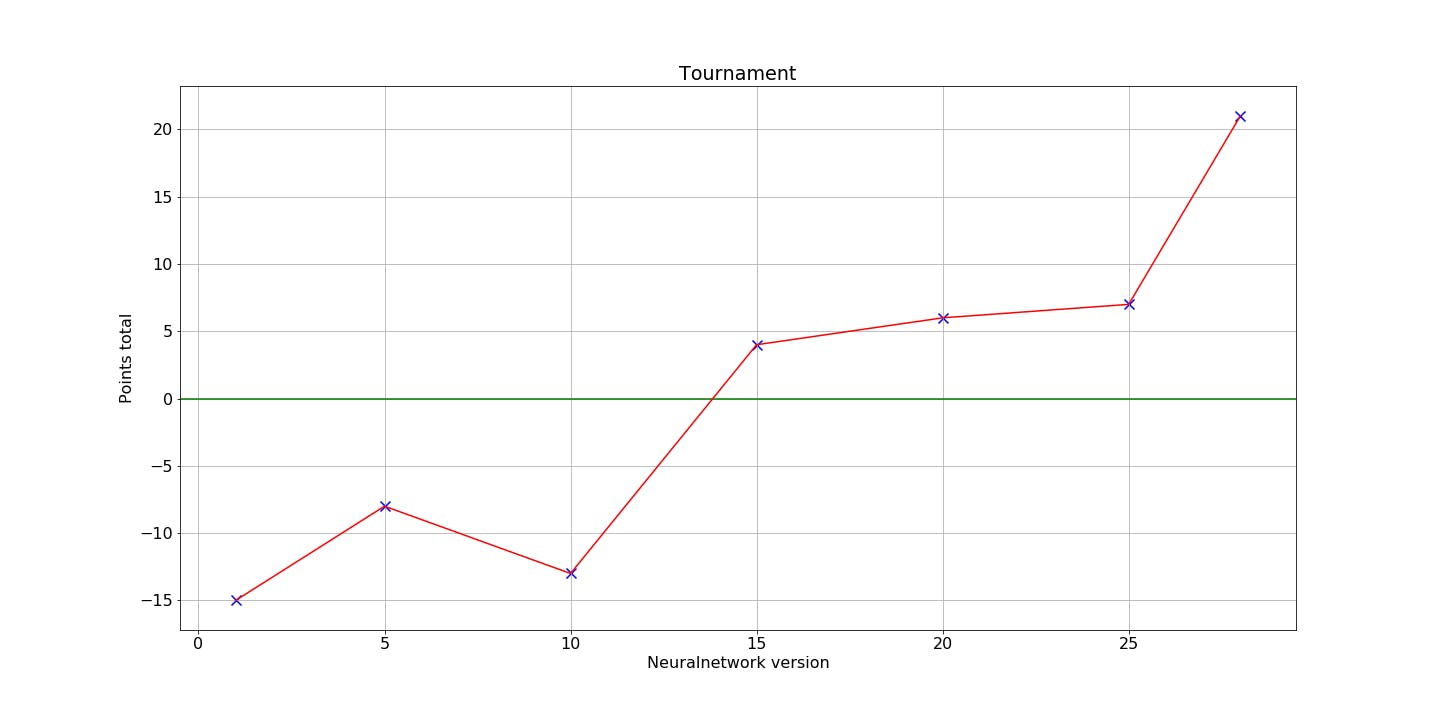
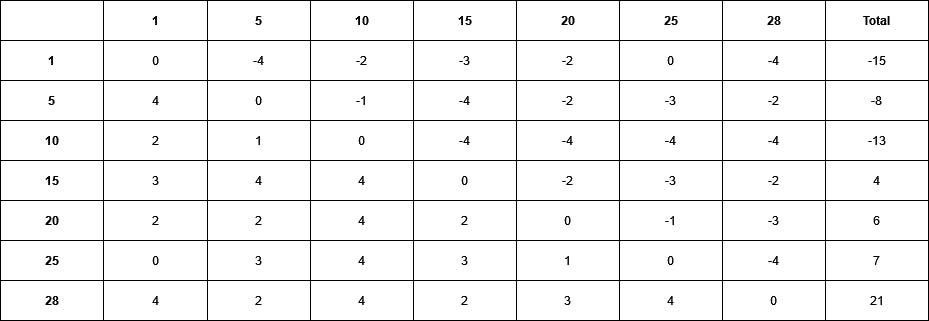
To evaluate the method at different stages of the learning process 28 players competed in a tournament. Each player represents a different iteration and thus a different level of proficiency. During the tournament, each player plays every player four times and gains/loses points equal to its wins/loses respectively (draws result in 0 points). The graphic illustrates the expected result that players representing a later stage of learning generally perform better than those representing earlier stages.
Thank you for your attention and for reading our blog post! Our team, Jonas Bode, Tobias Hürten, Luca Liberto, Florian Spelter and Johannes Loevenich would appreciate your inspiring feedback!

